DIFFERENTIATION OF RAISE TO POWER FUNCTION
Derivative of lnx, derivative of log x², derivative of ey,derivative of 2ˣ, Differentiation of raise to power function an easy and short cut manners, differentiation of raise to power function.
Till Date we have learn to differentiate this question by taking log on both sides and then differentiate.
There is very long process to differentiate this types of functions .
But today we shall learn a different and an easiest method to differentiate such type of functions.
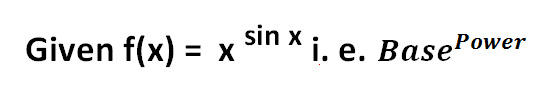
then assume this function as [ log (Base) ]× [ Power ] then use product rule of differentiation and place the given function in front of the result so obtained.
Question : Differentiate f(x) = (cos x )sin x
∴ h(x) = (log cos x) ×(sin x)
then it derivative will be
f '(x) = h'(x)
Therefore f '(x) = f(x) [(log cos x) . cos x + sin x (- sin x ) /cos x)]
Therefore f '(x) = (cos x )sin x [(log cos x) . cos x - sin x .tan x]
Question : How to solve this f(x) = x sin x
 { log x . sin x }= ( log x)
{ log x . sin x }= ( log x) ( sin x ) + ( sin x )
( sin x ) + ( sin x ) ( log x)
( log x)= log x . cos x + sin x . (1/x)
Now put f(x) in front of this result and that will be derivative of the f(x).
Hence f ' (x) = x sin x { log x . cos x + sin x . (1/x) }
Question : Differentiate w.r.t. 'x'
f(x) = cos x sin x + (sin x) xLet f(x) = g(x) + h(x)
Then f '(x) =g'(x) + h'(x)
Just place cos x sin x in front of derivative of {(log cos x) . (sin x) } + place (sin x) x in front of derivative of { ( log sin x) . ( x) },
So Answer will be
Similarly derivative of h(x) = (sin x) x in one step can also be written as
h '(x) = (sin x) x [ log sin x × 1+ x . cos x/sin x ]

Question : Differentiate f(x) = e sin x
then using short cut method,
f '(x) = e sin x [ log e × cos x ] ,
f '(x) = cos x .e sin x
f '(x) = cos x .e sin x
Because derivative of log e is zero and log e is equal to one
Question : Differentiate f (x) = a sin x
If f (x) = a sin x
then using short cut method ,
Question : Differentiate f (x) = x sin x + cos x
then using short cut method ,
f '(x) = x sin x + cos x [ log x . {cos x - sin x} + {sin x+cos x }.{1/x} ]
One more shortcut for differentiation you can use
Differentiation of Trigonometric Functions
S N f(x)
f '(x)
1
sin x
cos x
2
cos x
-sin x
3
tan x
sec²x
4
cot x
-cosec²x
5
sec x
sec x tan x
6
cosec x -cosec x cot x
| S N | f(x) | f '(x) |
|---|---|---|
| 1 | sin x | cos x |
| 2 | cos x | -sin x |
| 3 | tan x | sec²x |
| 4 | cot x | -cosec²x |
| 5 | sec x | sec x tan x |
| 6 | cosec x | -cosec x cot x |
Conclusion
Thanks for devoting your valuable time for this post differentiation of raise to power function,derivative of lnx, derivative of lnx²,derivative of e^y, derivative of 2ˣ, implicit function differentiation, derivative of logarithmaetic functions of my blog . If you liked this this blog/post, Do Follow me on my blog and share this post with your friends . We shall meet again in next post with solutions of most interesting and mind blowing mathematics problems ,till then Good Bye.













No comments:
Post a Comment
Your valuable suggestions are always acceptable to us for betterment of this website