Solving the system of Linear Equations of two variables
To Solve the system of Linear Equations using 2×2 Matrix Method
x - 5y = 4
2x + 5y = −2
x - 5y = 4
2x + 5y = −2
AX = B
where X = A-1 B------------------------(1)

Where
We need the inverse of A ( i. e. A-1 ), To find the inverse of Matrix A ,1st find out Co-factor Matrix of A
As we know the Ad joint Matrix of any matrix can be found by taking the transpose of the Co Factor matrix.
Therefore A-1 Exists ,So
Now putting the value of ( A-1 ) inverse of Matrix A in equation (1)
Now putting the elements of Matrix X , and
By the equality of two Matrices ,their elements in respective positions must be equal to each others,
Hence x= 2/3 and y = -2/3
How to check the correctness of a solution
put x= 2/3 and y = -2/3 in the given equations
x - 5y = 4 implies 2/3 - 5(-2/3) = 2/3+10/3 = 4and 2x + 5y = -2 implies 2×(2/3) + 5(-2/3) = 4/3-10/3 = -6/3= -2
therefore both equations are satisfied by these values of 'x' and 'y'
To Solve the system of Linear Equations using 3×3 Matrix Method
2x + y - 3z = 0
x + y + z = 2
Converting this system of Linear equations into Matrix Form
AX = B
X = A-1B ------------------------(1)
Where
Now we have to find the A-1. , and it will exist if its determinants value |A| is non Zero. Let us find |A|
|A|= 1{1×1-(-3)×1}-(-1){2×1-(3)×1}+1(2×1-1×1)
|A|= 1 {1+3}+1 {2+3}+1 {2-1}
|A|= 4+5+1 = 10
Since |A| is non Zero , Therefore A-1 (inverse of A ) exists .
We have to find the Co factors of all the elements of matrix A . Let us find out the co factors of all the elements of matrix row wise.
Co-Factors of 1st Row
co-factor of A11 = 4
co-factor of A12 = -5
co-factor of A13 = 1
co-factor of A23 = -2
co-factor of A31 = 2
co-factor of A32 = 5
co-factor of A33 = 3
Now co Factor matrix of A can be written as follows

Now to find the Ad joint of this Matrix, Take the transpose of this Matrix,

As we know the Inverse of a Matrix is the scalar multiplication of Ad Joint Matrix of Matrix A and reciprocal of Determinant value of the Matrix A.
Where
Now we have to find the A-1. , and it will exist if its determinants value |A| is non Zero. Let us find |A|
|A|= 1{1×1-(-3)×1}-(-1){2×1-(3)×1}+1(2×1-1×1)
|A|= 1 {1+3}+1 {2+3}+1 {2-1}
|A|= 4+5+1 = 10
Since |A| is non Zero , Therefore A-1 (inverse of A ) exists .
We have to find the Co factors of all the elements of matrix A . Let us find out the co factors of all the elements of matrix row wise.
Co-Factors of 1st Row
co-factor of A12 = -5
co-factor of A13 = 1
Co-Factors of 2nd Row
co-factor of A21 = 2
co-factor of A22 = 0co-factor of A23 = -2
Co-Factors of 3rd Row
co-factor of A31 = 2
co-factor of A32 = 5
co-factor of A33 = 3
Now co Factor matrix of A can be written as follows

Now to find the Ad joint of this Matrix, Take the transpose of this Matrix,

As we know the Inverse of a Matrix is the scalar multiplication of Ad Joint Matrix of Matrix A and reciprocal of Determinant value of the Matrix A.
Putting the values of Inverse of A and Matrix B in equation (1), So after Multiplication of these two matrices ,we get

Now putting the values of elements of Matrix X, and equating the elements in their respective positions .

Now using the property of equality of two Matrices , All the elements in their respective position are equal to each other , we get
x = 2 , y = -1, z = 1 is the solution of the system of linear Equations.
Conclusion
In this post I have discussed the method of solving the System of linear Equations with the help of Matrix Method ,method to find inverse of a matrix .,Matrices and Determinants in Most imp,How to find inverse of 3x3 Matrix, how to solve determinant,how to solve system of equation by matrix,matrix method of solving system of equations of three variables,determinant of 3x3 matrix calculator, matrices and determinants in most imp,If you liked the post please share it with your friends , And in case of any improvement please make use of Comment Box . To keep on supporting me follow my Blog . Thanks for your valuable time to read this post .We shall meet you in next post ,till then BYE.







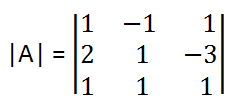


No comments:
Post a Comment
Your valuable suggestions are always acceptable to us for betterment of this website