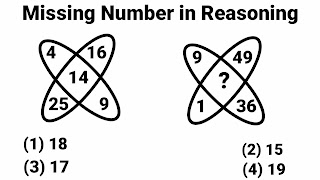Missing number in box Reasoning problem, How to solve various circle problems

Reasoning of missing number in box problems, circle problems  and triangle problems will be discussed with the help of 10 most important examples. Some of these examples are of  4 × 4  order and other are of  4 × 3 orders. 

Reasoning of missing number in box problems in Uniteted State

PROBLEM #  1

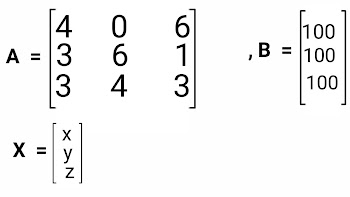
Formula

Every row has been written as the cube of certain number. Because 4096 is the cube of 18, 6859 is the cube of 19 , 8000 is the cube of 20  similarly 926? will also be  the cube of any number. Look carefully 1st row is the cube of 18, then 2nd row is the cube of 19, 3rd row is the cube of 20 . So in this way 4th row must be  the cube of 21.

Calculation

18³ = 4096 

19³ = 6859 

20³ = 8000

21³ = 9261

Hence value of question mark will be 1.

Option (D)1 is correct option.

PROBLEM #  2 

  

Formula

Multiply the number in 2nd row with 100 and add it to the product of numbers in 1st and 2nd rows.

Calculation

6*100 + (4*8) = 632

3*100 + (9*2) = 318

7*100 + (5*9) = 745

 Option (A)745 is correct option.

PROBLEM #  3 

This reasoning problem consists of three figures and every figure have three numbers associated to it . Two numbers are on the upper line of each box and one number is at the bottom of the dark box.  Look at last figure , it have ? in its centre . So the solution of this problem is to find the value of question mark using two numbers associated to it . 

          But the main problem is how to utilised  these two numbers to get the value of question mark?

          Now watch carefully the 1st two figures . Since these figures have some values of numbers in dark box . 

          Now we have to find or search the  formula for these three numbers in each figure to utilised them in any possible way to get number in  dark box . 

         The same formula will be applicable to third figure to find out the value of question mark.

Formula :- The DIFFERENCE of squares of both the numbers in empty box in upper line in every figure is equal to  number in dark box in lower line.

Solution:- 

9²  - 6² = 81 - 36 = 45 (1st Figure)

8²  - 2² = 64 - 4 = 60 (2nd Figure)

7²  - 3² = 49 - 9 = 40  (3rd Figure)

Option (1)40  is correct option.

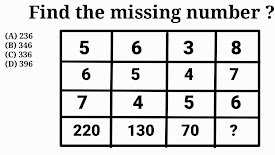
PROBLEM #  4 

This reasoning problem consists of three figures and every figure have three numbers associated to it . Two numbers are on the upper line of each box and one number is at the bottom of the dark box.  Look at last figure , it have ? in its centre . So the solution of this problem is to find the value of question mark using two numbers associated to it . 

          But the main aim is how to utilised  these two numbers to get the value of question mark?

          Now watch carefully the 1st two figures . Since these figures have some values of numbers in dark box . 

          Now we have to find or search the  formula for these three numbers in each figure to utilised them in any possible way to get number in  dark box . 

         The same formula will be applicable to third figure to find out the value of question mark.

Formula :- The SUM of squares of both the numbers in empty box in upper line in every figure is equal to  number in dark box in lower line. 

Solution:- 

9²  + 6² = 81 + 36 = 117 (1st Figure)

8²  + 2² = 64 + 4 = 68 (2nd Figure)

7²  + 3² = 49 + 9 = 58 (3rd Figure)

Option (1)58 is correct option

PROBLEM #  5 

This figure consist of four squares around  one big square. Look carefully in this big square every number in it is perfect cube. And if we multiply the square roots of  two adjacent numbers then we shall have the number attached to big square between these two numbers whose square root had been multiplied.

√49  ×  √4 =  7  × 2 = 14 (The number at bottom line in the box)

√4  ×  √36 =  2  × 6 =  12 ( The number at leftmost box )

√36  ×  √? =   6  × √? = 30 ( The number at uppermost box )

√?  = 30/6 = 5, squaring both sides

? = 25 ( The number at uppermost box)

Similarly

√?  ×  √49 = 35 

√?  = 35/7

√?  = 5,  squaring both sides

? = 25  (The number at rightmost box )

 Option (A)25  is correct option

Also Reads these articles

 Latest-Questions-of-missing-numbers 

 Reasoning for competitive exams

  Reasoning for bank exams
 Missing  number series questions
 Circle Reasoning
 15 Questions Circle Problems  

PROBLEM # 6

This figure consist of four squares around  one big square. Look carefully in this big square every number in it is perfect cube. And if we multiply the square roots of  two adjacent numbers then we shall have the number attached to big square between these two numbers whose cube root had been multiplied.

∛343  ×  ∛27 =  7 × 3 = 21( The number at rightmost box )

∛27  ×  ∛125 =  3  × 5 = 15 (The number at bottom line in the box)

∛125  ×  ∛? =  5  ×   ∛? = 10 ( The number at leftmost box )

5  ×  ∛? = 10 

 ∛?  = 10/5

 ∛? = 2 , cubing both sides

? = 8

Similarly

∛?  ×  ∛343 =   ∛?  × 7  = 14

 ∛? = 14/7 = 2 cubing  both sides

? = 8 ( The number at uppermost box )

Option (C)8  is correct option

PROBLEM #  7 

This reasoning problem have two figures and every figure have five number attached to it . Four numbers are at the corner of each figure and one number is at the middle of the same figure.

       Since second figure have question mark in its centre . So the solution of this problem is to find the value of question mark using four numbers associated to it . 

          But the main problem is how to utilised these four numbers to get the value of this question mark?

          Now watch carefully the 1st two figures . since these figures have some values of middle numbers. 

          Now we have to find or search the  formula for these four numbers in each figure to utilised them in any possible way to get middle or central number. 

         The same formula will be applicable to third figure to find out the value of question mark.

Formula:-   Add all the numbers in the corner of each figure  to get value of the number in the middle.

Solution:-

√4 + √16 + √9 + √25 + √4 = 2 + 4 + 3 + 5 = 14 (Middle number in 1st figure).

√9 + √49 + √36 + √36 + √1 = 3 + 7 + 6 + 1 = 17 (Middle number in 1st figure).

Option (3)17  is correct option

Reasoning of missing number in circle problems

PROBLEM #  8

This circle consists of four quadrants and every  quadrant consists of three numbers . And every quadrant have two numbers in outer part and one  number  in the inner part . To find the value of question mark  "?"  , we shall use two numbers which are in the outer part to calculate the value of the number which is in the inner part of every quadrant . 

1st Quadrant 

Step 1.   Take sum of the squares of both the numbers (8 and 4 ) in outer part of  this quadrant.

Step 2. Take the magnitude of difference of both the numbers in outer part of  this quadrant.

Step 3. Divide the result obtained in step 1 with the result obtained in step 2 to get the value of the number (20) in inner part of this quadrant.

Calculation

(8² + 4² ) ÷ ( |8 - 4 |) = ( 64 + 16 ) ÷ 4 = 80 ÷ 2 = 20

2nd Quadrant

Step 1.   Take sum of the squares of both the numbers ( 7 and 5 ) in outer part of  this quadrant.

Step 2. Take the magnitude of difference of both the numbers in outer part of  this quadrant.

Step 3. Divide the result obtained in step 1 with the result obtained in step 2 to get the value of the number (37) in inner part of this quadrant.

Calculation

(5² + 7² ) ÷ (|5 - 7 |) = ( 25 + 49 ) ÷ 2 = 74 ÷ 2 = 37

3rd Quadrant

Step 1.   Take sum of the squares of both the numbers ( 10 and 6 ) in outer part of  this quadrant.

Step 2. Take the magnitude of difference of both the numbers in outer part of  this quadrant.

Step 3. Divide the result obtained in step 1 with the result obtained in step 2 to get the value of the number (34) in inner part of this quadrant.

Calculation

(10² + 6² ) ÷ ( |10 - 6| ) = ( 100 + 36 ) ÷ 4 = 136 ÷ 4 = 34

4th Quadrant

Step 1.   Take sum of the squares of both the numbers ( 10 and 6 ) in outer part of  this quadrant.

Step 2. Take the magnitude of difference of both the numbers in outer part of  this quadrant.

Step 3.  Divide the result obtained in step 1 with the result obtained in step 2 to get the value of the number (34) in inner part of this quadrant.

Calculation

(6² + 4² ) ÷ ( |6 - 4 |) = ( 36 + 16 ) ÷ 2 = 52 ÷ 2 = 26

Option (3)26 is right option

Also Reads these articles

Maths logical reasoning Q & A

Reasoning for competitive exams
 Reasoning for bank exams
Ten Tricky logical reasoning
 Reasoning questions with answers
  Box Problems 

PROBLEM #  9 

This  big circle is  divided into eight parts and  there is also one number written between  any  two numbers towards outer side of these two numbers .  If we  add these  two adjacent  numbers then reverse of order of the result so obtained then this number will be equal to the number in small circle opposite to both these numbers .

8  +  6  = 14 ⟺  41 ( Reversing the order of digits) 

6 + 11 = 17 ⟺  71  ( Reversing the order of digits)

11 + 10 =  21 ⟺ 12 ( Reversing the order of digits)

10 + 31 = 41 ⟺ 14 ( Reversing the order of digits)

31 + 12 = 43 ⟺ 34 ( Reversing the order of digits)

12 + 17 = 29 ⟺ 92 ( Reversing the order of digits)

17 + 5  = 22 ⟺ 22 ( Reversing the order of digits)

8  + 5 = 13  ⟺  31 = ? ( Reversing the order of digits)

Hence the value of  "? " will be 31 

Option (B)13 is right option

Reasoning of missing number in triangle problems

PROBLEM #  10 

This reasoning problem consists of three figures and every figure have three numbers associated to it . So the solution of this problem is to find the value of question mark using other two numbers associated to it . 

          But the problem is how to utilised these two numbers to get the value of this question mark?

          Now we have to find or search the  formula for these two numbers in each figure to utilised them in any possible way to get third number. 

         The same formula will be applicable to third figure to find out the value of question mark.

Formula :- One tenth of the product of  two outer numbers in each triangle is equal to third number .

 1st Triangle

( 5 × 4 ) ÷ 10 = 20 ÷ 10 = 2 (Middle number in 1st triangle ) 
2nd Triangle

( 6 × 5 )  ÷ 10 = 30 ÷ 10 = 3 (Middle number in 2nd triangle ) 
3rd Triangle 

( 15 × 6 )  ÷ 10 = 90 ÷ 10 = 9 (Middle number in 3rd triangle ) 

Option (3)9  is correct option

Ten Most Important Reasoning questions with answers for competitive exams of  series , box and other type with solutions have been discussed in this post . These types of problems are very helpful for cracking competitive exams like ssc cgl, ssc chsl and various Bank exams and many other similar exams. please feel free to comment your opinions

Read More

Inverse method of solving linear equations of three variables

Inverse method of solving linear equations of 3 variables

Matrix method of solving linear equations of three variables with the help of example. 

Set of given equations are 

4x + 6z = 100     --------------------------------> (1)

3x + 6y + z = 100   -----------------------------> (2)

3x + 4y + 3z  = 100   ---------------------------> (3)

The system of these equations can be transformed into Matrix formed 

AX =  B  ,  ⇒ X =   A^-1 B    -------------------------->  (*)

Where A is matrix written from the coefficients of x, y and z when these equations are in symmetric form and B is the matrix written from constants from right hand sides in column form and X is matrix of all the variables in column form. 

In order to find the solution of set of these equations , first we have to find the inverse of matrix A if it exist then we can find the solution otherwise Matrix method fails to find the solution of the set of linear equations . 

Evaluation of Determinant 

|A|  = 4 (18 - 4) -0(9 - 3) +6(12 - 18)

       =  4(14) + 0 + 6(-6) 

       = 56 - 36

        = 20

Since the determinant value of this matrix  is not equal to zero ,Therefore its inverse can be calculated.

And  formula for finding the inverse of matrix A is 

Where Adjoint A is the transpose of co factor matrix. And in order to find the co factor matrix of any matrix, we have to find co factors of all the elements present in this matrix. 

How to calculate  co factors of all the elements of the matrix A

Let us calculate these cofactors.  

Now these co factors can be written in matrix form known as co factor Matrix. 

Co factors of 1st row are  (18 - 4) , -(9 - 3), (12 - 18) 

i. e. Co factors of 1st row are 14, -6 , -6

Co factors of 2nd row are -(0 -24), (12 - 18) , -(16 - 0) 

I. e. Co factors of 2nd row are  24 , -6 , -16

Co factors of 3rd row are  (0 - 36), -(4 - 18), (24 - 0) 

i.e. Co factors of 3rd row are  -36 , 14 , 24

Co factor Matrix

Writing co factors of 1st row in 1st row of this matrix , co factors of 2nd row in 2nd row of this matrix . Similarly co factors of 3rd row in 3rd row of this matrix . 

Adjoint  Matrix

To find the Ad joint of this matrix we have to take it's transpose, Because transpose of any matrix is called Ad joint of the matrix. So writing all the elements which are in 1st row in 1st column, and  all the elements which are in 2nd row in 2nd column and  all the elements which are in 3rd row in 3rd column. 

Inverse  Matrix

Now we can find inverse of the matrix A by putting the value of inverse of A in equation  (4), we get

Now  putting the values  Matrix B and    A^-1  in (4) 

After simplification and using the properties of equality of two matrices  ( Two matrices of same order are equal iff their respective elements are equal to each other ) 

⇒  x = 10

     y  = 10

      z = 10

So this was the Matrix method of solving linear equations of three variables using inverse of matrix. Your valuables comments will be appreciated for betterment of this blog.

Read More

Missing number Reasoning SSC CGL questions and answers

Ten most Missing number Reasoning SSC CGL questions and answers for competitive exams, reasoning questions with answers for bank exams, Reasoning tricks for competitive exams have been discussed in this article for upcoming competitive exams. 

10 Most Important Reasoning Problems for competitive Exams

Question #1

Misiing Number 

Since the question mark is in the 3rd figure. So the value of question mark will be calculated with the help of remaining four numbers in the 3rd figure in the same way, the middle numbers have been calculated in 1st and 2nd figure with the help of remaining four numbers. This question mark value can be found by this method.   

Formula:-

Sum of four numbers = Product of both the digits in middle number.

Calculation:-

7 + 4 + 7 + 12 = 30 = 5 × 6  = Multiplication  of 5 and 6 (Middle number in 1st figure ) 

15 + 7 + 12 + 8 = 42 = 6 × 7 = Multiplication  of 6 and 7 (Middle number in 2nd figure ) 

11 + 18 + 5 + ? =  ????  = 6 × 6 = Multiplication  of 6 and 6(Middle number in 3rd figure ) 

⇒ 34 + ? = 36

⇒  ? = 36 - 34

⇒  ? = 2

 Hence option (1)2 is correct.

Question #2

Since the question mark is in the 3rd figure. So the value of question mark will be calculated with the help of remaining four numbers in the  figure in the same way, the middle numbers in 1st and 2nd figure can be calculated with the help of remaining four numbers around each figure. This question mark value can be found by this method.

1st Circle

8 + 4 + 3 + 1 = 16 (Greatest number in 1st circle) 

or 

16 - (8 + 4 + 3) = The number in the middle of circle

16 - 15 = The number in the middle of circle

1  =  The number in the middle of circle

2nd Circle

4 + 3 + 5 + 8 = 20 (Greatest number in 2nd circle)

or 

20 - (4 + 3 + 5) = The number in the middle of circle

20 - 12 = The number in the middle of circle

8  =  The number in the middle of circle

3rd Circle

6 + 4 + 5 + ? = 18 

⇒ 15 + ? = 18

⇒ ? = 18 - 15

⇒ ? = 3 (Greatest number in 3rd circle)

This will be the value of question mark.

or 

18 -  (6 + 4 + 5 ) = The number in the middle of circle

18 - 15 = The number in the middle of circle

3 =  The number in the middle of circle

Hence option (1)3 is correct.

 

Question #3

Starting from 4th quadrant in anticlockwise direction , add one to the sum of squares of both the numbers in outer part of the quadrant to get the value of the number in the inner part of same quadrant.

4th Quadrant

(2 + 8)² + 1 =  10²  + 1 =  100 + 1 = 101

1st Quadrant

(3 + 8)² + 1 =  11²  + 1 = 121 + 1 = 122

2nd Quadrant

(7 + 1)²  + 1 =   8² + 1 = 64 + 1 = 65

3rd Quadrant

(5 + 4)² + 1 =   9²  + 1 = 81 + 1 = 82 (The value of question mark)

Hence option (1)82  is correct.

Question #4

Starting from 4th quadrant in anticlockwise direction , Subtract one from the sum of squares of both the numbers in outer part of the quadrant to get the value of the number in the inner part of same quadrant.

4th Quadrant

(2 + 8 )² - 1 =  10²  + 1 =  100  - 1 = 99

1st Quadrant

(3 + 8)² - 1 =  11²  + 1 = 121 - 1 = 120

2nd Quadrant

(7 + 1 )²  - 1 =   8² + 1 = 64 - 1 = 63

3rd Quadrant

(5 + 4 )² - 1 =   9²  + 1 = 81 - 1 = 80 (The value of question mark)

Hence option (2)80  is correct.

Question #5

Since the question mark is in the 3rd figure. So the value of question mark will be calculated with the help of remaining four numbers in the  figure in the same way, the middle numbers in 1st and 2nd figure can be calculated with the help of remaining four numbers around each figure. This question mark value can be found by following method.

1st Figure

63 + 34  +  8  = 105 (Greatest number in 1st figure) 

or 

105 - (63 + 34) = The number in the middle of 1st figure

105 - 97 = The number in the middle of 1st figure

8  =  The number in the middle of 1st figure

2nd Figure

30 + 10 + 5  =  45 (Greatest number in 2nd figure) 

or 

45 - (30 + 10) = The number in the middle of 2nd figure

45 - 40 = The number in the middle of 2nd figure

5  =  The number in the middle of 2nd figure

3rd Figure

31 + 62 + ? = 121 This implies ? = 28 (Greatest number in 3rd figure) 

or 

121 - (62 + 31) = The number in the middle of 3rd figure

121 - 93 = The number in the middle of 3rd figure

28  =  The number in the question mark in 3rd figure

Hence option (4)28  is correct.

Also Reads these articles

 Latest-Questions-of-missing-numbers 

Maths logical reasoning Q & A

Reasoning for competitive exams
Box and circle reasoning
 Reasoning for bank exams
Ten Tricky logical reasoning 

Question #6

This circle has been divided into four quadrants and each quadrant is composed of three numbers . In each quadrant two numbers are in outer quadrant of the circle and one number is in the inner quadrant of the circle. 

Starting from fourth quadrant in clockwise direction. 

Formula : - Half of sum of the squares of both the numbers in outer sector is equal to inner sector.

 4th Quadrant

( 8² + 6²)/2 = ( 64 + 36)/2 = 100/2  =50 (Number in the inner part of the circle in 4th quadrant )

 3rd Quadrant

( 7² + 5²)/2 = ( 49 + 25)/2 = 74/2  = 37  (Number in the inner part of the circle in 3rd quadrant )

 2nd Quadrant

( 10² + 8²)/2 = ( 100 + 64)/2 = 164/2  = 82 (Number in the inner part of the circle in 2nd quadrant )

 1st Quadrant

( 9² + 11²)/2 = ( 81 + 121)/2 =  202/2  = 101 (Number in the inner part of the circle in 1st quadrant  ).

And 101 will be the value of question mark.

Hence option (4)101  is correct.

Question #7

This circle has also been divided into four quadrants and each quadrant is composed of three numbers . In each quadrant two numbers are in outer sector of the circle and one number is in the inner sector of the circle. 

Starting from 1st quadrant in clockwise direction. 

Formula : -  Sum of the squares of both the numbers in outer sector is equal to inner sector.

  1st Quadrant

(3 + 5)² = (8)² = 64  (Number in the inner part of the circle in 1st quadrant )

 2nd Quadrant

(5 + 4)² = (9)² = 81  (Number in the inner part of the circle in 2nd quadrant )

 3rd Quadrant

(4 + 2)² = (6)² = 36  (Number in the inner part of the circle in 3rd quadrant )

 4th Quadrant

(6 + 4)² = (10)² = 100  (Number in the inner part of the circle in 4th quadrant ).

And 100 will be the value of question mark.

 

Question #8

This box problem consists of three rows and three columns. To find the value of question marks in 3rd column of 3rd row, we have to add 1st ,2nd and 3th columns since since in every column is same in every row.

Formula :- The sum of 1st three columns in every row is same .

7 + 8 + 15 = 30 ( 1st  row) 

9 + 20 + 1 = 30 (2nd row) 

14 + 2 + ? = 30 ( Because sum of all the three digits in 3rd row must be equal to the sum in other two rows)

Hence  16 + ? = 30

⇒ ? = 30 - 16 

⇒  ? = 14

Therefore the value of question mark is 14

Hence option (B)14  is correct.

Question #9

This box problem consists of four rows and four columns. To find the value of question marks in 3rd column of 3rd row, we have to divide the sum of  1st ,2nd and 3th rows with 4 to get the value of number in 4th row.

Formula :- The one fourth of  the sum of 1st three rows in every column.

5 + 8 + 7  = 20 ÷ 4 = 5 ( 1st column  in 4th row) 

9 + 6 + 13 = 28 ÷ 4 = 7 (2nd column in 4th row) 

(7 + 10 + 19) ÷ 4  = 36 ÷ 4 = 9 (4th column in 4th row) 

(8 + 9 + ?) ÷  4 =  8  (3rd column in 4th row) 

⇒ 17 + ?  =  8  ×  4

⇒ ? = 32 - 17

⇒ ? = 15

Hence option (D)15  is correct.

Also Reads these articles

Missing  number series questions
Reasoning questions with answers
Circle Reasoning
 Box Problems
15 Questions Circle Problems 
 SSC CGL Reasoning

Question #10

This box problem consists of four rows and four columns. To find the value of question marks in 4th column of  fourth row, we have to multiply 1st ,2nd and 3th rows  at the same time and then add 10 to the result so obtained. 

Formula :- Ten more than the product of 1st three rows in every column.

(5 × 6 × 7 )  + 10 = 210 + 10 = 220 (1st column  in 4th row) 

(6 × 5 × 4 )  + 10  = 120 + 10 = 130 (2nd column in 4th row)

(3 × 4 × 5 )  + 10  =  60 + 10 = 70 (3rd column in 4th row) 

(8 × 7 × 6 )  + 10  = 336 + 10 = 346 (4th column in 4th row) 

Hence option (B)346  is correct.

In this post I discussed Ten Missing number Reasoning SSC CGL all questions and answers . Comment your valuable suggestion for further improvement.

Also Read these posts on Reasoning

ReasoningProblems #11  

ReasoningAnalogy #10

Reasoning Questions #9    
Circle Reasoning #8
TenBox-Problems #7   
TenReasoning problems #6
Ten-Important-Problem#5  
Ten--Tricky-Puzzles #4
Twelve-Figures-Problems#3   
Ten-Important-Reasoning#2     
Picture-Reasoning#1

Read More

Matrix method of solving linear equations of three variables

Learn the process of solving linear equations of three variables by matrix method  .Let us understand this method with the help of an example

Matrix method of solving linear equations of 3 variables

Matrix method of solving linear equations of three variables with the help of an example. 

The system of these equations can be transformed into Matrix form as 

AX =  B  ,  ⇒ X =   A^-1 B   ->  (*)

Where A is matrix written from the coefficients of x, y and z when these equations are in symmetric form and B is the matrix written from constants from right hand sides in column form and X is matrix of all the variables in column form. 

In order to find the solution of set of these equations , first we have to find the inverse of matrix A if it exist then we can find the solution otherwise Matrix method fails to find the solution of the set of linear equations . 

Evaluation of Determinant 

|A|  = 1 (-9 - 27) -1(6 - 63) -1(6 + 21)

       =  -36 + 57 - 27

       = -63 + 57

        = -6

Since the determinant value is not equal to zero ,Therefore its inverse can be calculated.

And  formula for finding the inverse of matrix A is 

Where Adjoint A is the transpose of co factor matrix. And in order to find the co factor matrix of any matrix, we have to find co factors of all the elements present in that matrix. 

How to calculate  co factors of all the elements of the matrix A. 

 Let us calculate these cofactors. 

Co factors of 1st row are  -36 , 57 , 27

Co factors of 2nd row are  -6, 10 , 4

Co factors of 3rd row are  6 . -11 , -5

Now these co factors can be written in matrix form known as co factor Matrix. 

Co factor Matrix

Writing co factors of 1st row in 1st row of this matrix , co factors of 2nd row in 2nd row of this matrix . Similarly co factors of 3rd row in 3rd row of this matrix . 

Adjoint  Matrix

To find the Ad joint of this matrix we have to take it's transpose, Because transpose of any matrix is called Ad joint of the matrix. So writing all the elements which are in 1st row in 1st column, and  all the elements which are in 2nd row in 2nd column and  all the elements which are in 3rd row in 3rd column. 

Now we can find inverse of the matrix A by putting the value of inverse of A in equation  (4), we get

Now  putting the values  Matrix B and    A^-1  in (4) 

After simplification and using the properties of equality of two matrices  ( Two matrices of same order are equal if and only if their respective elements are equal to each other ) 

⇒  x = -54/-6 = 9

 y =  12/-6 = 2

 z  = -24/-6  = -4

Hence

 x = 9 

 y = 2

 z = -4

So this was the Matrix method of solving linear equations of three variables using inverse of matrix. Your valuables comments will be appreciated for betterment of this blog.

Also read this post for understanding inverse of matrix using elementary row transformation

 

Read More