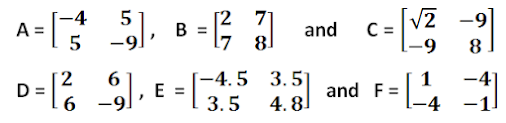How to find symmetric and skew symmetric matrices
How to find symmetric and skew symmetric matrices
CAN YOU SOLVE THIS PUZZLE ?
If you want to know the answer of this problem , just click here
At the end of this post, we shall be able to solve or crack this type of quiz, puzzle, or brain teaser.
Let us discuss symmetric and skew symmetric Matrices, How to know whether any given matrix is symmetric or skew symmetric and How to construct 2 × 2 and 3 × 3 Matrix which are Symmetric Matrix And Skew Symmetric Matrix. Before we proceed we must know what is Transpose Of a Matrix .
Symmetric Matrix
Any square matrix is said to Symmetric Matrix if the transpose of that Matrix is equal to the matrix itself. That is if we transform all the Rows of the Matrix into respective column, even then we get same Matrix . Let us discuss this with the help of Some Examples.
1 Complete the 1st Row of the matrix with the elements of your
choice.
2 Copy all Elements which are in 1st Row to 1st Column.
3 Now place last element in
2nd Column of 2nd Row with your choice.
The Matrix so obtained is Symmetric Matrix.
As Transpose of these Matrices are equal the Matrices itself, Therefore these Matrices are Symmetric Matrix .
How to Construct 3 × 3 Symmetric Matrix
1 Complete the 1st Row of the matrix with the elements of your
choice.
2 Copy all
Elements which are in 1st Row to 1st Column.
3 Complete the 2nd Row of the matrix with the elements of your
choice.
4 Copy all
Elements which are in 2nd
Row to 2nd Column.
5
Put the last element
in the 3rd Column of 3rd
Row of your choice.
The Matrices so obtained are Symmetric
Matrices.
As Transpose of these Matrices are the Matrices itself, Therefore these Matrices are Symmetric Matrices.
Read Shortcut to find 2×2 and 3×3 Inverse Matrices in a easy way.
Skew Symmetric Matrix
Any square matrix is said to Skew Symmetric Matrix if the transpose of that Matrix is equal to the negative of the matrix. That is if we transform all the Rows of the Matrix into respective columns, even then we get same matrix with change in magnitude. Let us discuss this with the help of Some Examples.
Watch this video to better understand this concept of symmetric and skew symmetric Matrix
How to Construct 2 × 2 Skew Symmetric Matrix
1 Put all the elements equal to Zero in diagonal positions.
2 Complete the 1st Row of the matrix with the elements of your
choice.
3 Copy all Elements which are in 1st Row
to 1st Column with change in magnitude of each element.
The Matrix so obtained is Skew Symmetric Matrix
As Transpose of each of the Matrix written above is negative of the Matrix itself, Therefore these Matrices are Skew Symmetric Matrices.
How to Construct 3 × 3 Skew Symmetric Matrix
1 Complete all Diagonal elements of the Matrix with Zero.
2 Complete the
remaining elements the 1st
Row with your Choice
3 Copy all Elements which are in 1st Row
to 1st Column.
4 Complete the
remaining elements of the 2nd
Row of the matrix with the elements of your choice.
5 Copy all Elements which
are in 2nd Row to 2nd Column with change in magnitude of every element.
6 As the elements in the 3rd column of 3rd
Row is already taken as Zero.
For 3 × 3 Matrix
The Matrices so obtained are Skew Symmetric Matrices, as the
negative of the Transpose of each Matrices are equal to the Matrices Constructed.
Conclusion
This post is about Symmetric Matrix And Skew Symmetric Matrix . How to Identify and construct 2 × 2 and 3 × 3 Matrices which are Symmetric Matrix And Skew Symmetric Matrix .If you liked the post then share it with your friends and follow me on my blog to boost me to do more and more for you. We shall meet in next post ,till then BYE.....................